[10000印刷√] 正四角錐 高さ 求め方 161339-正四角錐 高�� 求め方
すると、球の体積は大量の半径rの高さの細かい四角錐の合計と考えられる。 「正方形の1辺の長さ」と「正四角錐の高さ」がわかっているパターン それぞれの求め方についてゆっくりみていこう。 あなたに最適な壁紙サイズは x です。数学「三平方の定理」 中学校・第3学年 Pythagorean MP 三平方の定理 応用問題・円周角の利用5 中学数学 練習問題プリント 表面積が1cm²である次の四角錐の側面の三角形の高さを求めましょう。 《側面の三角形の高さの求め方》 この四角錐の表面積は1cm²。 また底面積=7×7=49cm²であることが展開図よりわかります。 ここで、 四角錐の表面積=底面積+側面積 の公式より

四角錐公式 Mdsulja
正四角錐 高さ 求め方
正四角錐 高さ 求め方- 底面積×高さ÷3だと あ 4ヶ月前 ありがとうございます! 助かりました! ブドウくん 4ヶ月前 それは体積ではないでしょうか? 表面積は普通に展開図を考えて、底面の正方形と側面の三角形4つの面積を足せば求まるかと思います。 あ 4ヶ月前 ほんと〇 四角錐の体積は、底面積を求めて高さをかける、そして\(\times \frac{1}{3}\)を忘れないように! 四角錐の表面積 このように四角錐の展開図は、 四角形の底面、三角形4つ分の側面 になります。



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ
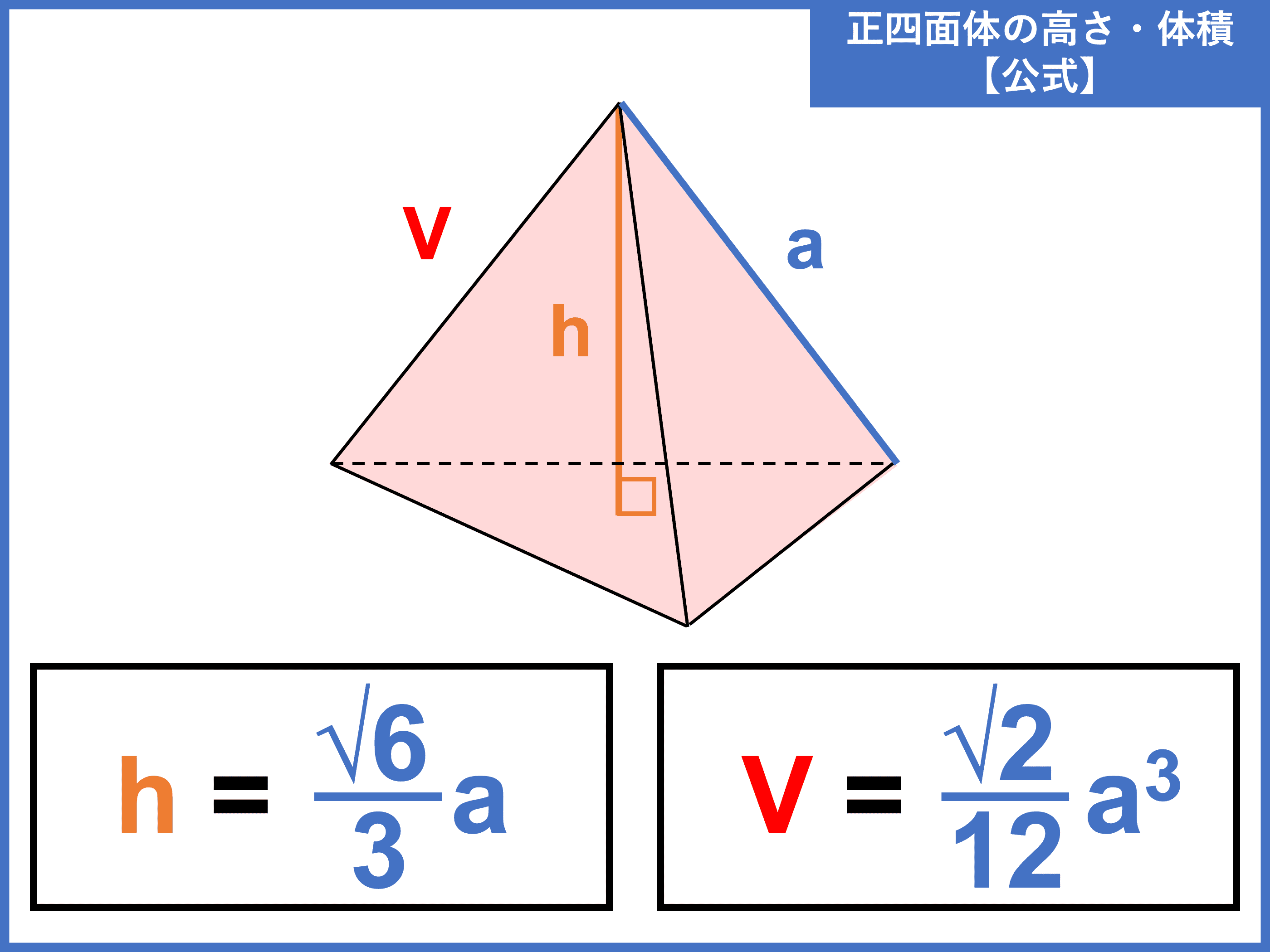
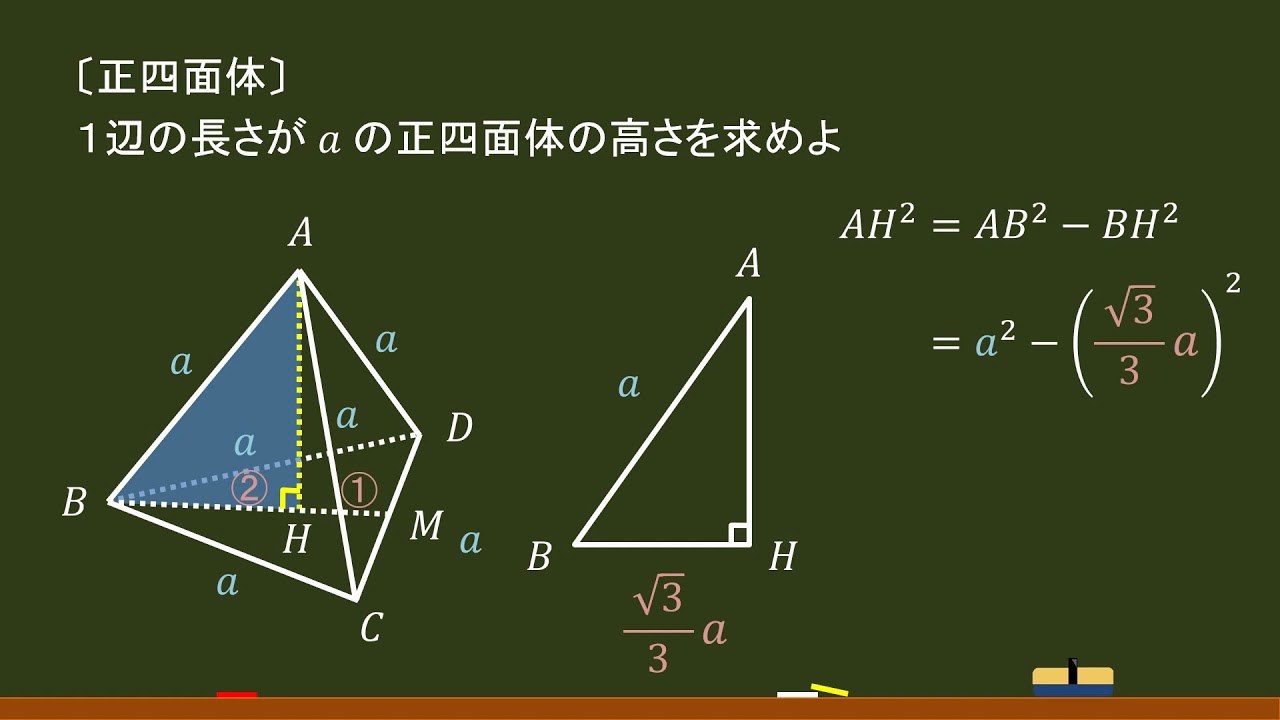
《四角錐の高さの求め方》 (底面は一辺が12cmの正方形) 四角錐の体積=底面積×高さ× より 四角錐の高さ=四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=12×12=144(cm²)であることから 求める四角錐の高さ=432÷144×3=9(cm)と「正四面体」 、つまり 「三角すい」 の体積を求めるよ。先のとがった、「すい」の体積の求め方って覚えているかな? (「すい」の体積)= (底面積)×(高さ)×1/3 だったね。 をするところに注意だ。 正四角錐 高さ 求め方 中1上の図を見てみよう。 「正四面体」とは、全ての面が 「正三角形」 、つまり、 辺 も、 角度 も、 すべて等しい 特別な四面体だよ。 この「正四面体」は、実はスゴい特徴を持っているんだ。 実は 「『1辺』 の長さが分かれば
正四角錐の体積の問題になります。 基本的な問題なのでできるようにしておきましょう。 問題6 図は1辺が6cmの正方形の周りに、それぞれの辺を底辺とし、高さが5cmの二等辺三角形を四枚並べてみたものである。 ビデオ 正四面体の体積の求め方 (1) 22, 四月 角錐は三次元形状であり、その各側面は三角形の形状を有する。 三角形もまた底辺にあり、すべての辺が同じ長さを持つ場合、これは正いよいよ体積 ようやく体積を求める準備が整いました。 この正四面体の高さ OH O H は下図のようになっています。 OH O H が何 cm c m なのか求めます。 当然、三角形 OAH O A H に三平方の定理を用います。 AM A M は 1 1 辺が 2cm 2 c m の正三角形の高さなので
代表的な \(2\) つの解き方を確認しておきましょう。 体積の利用 \(ce\) の長さは、底面を三角形 \(oab\) と見たときの 三角錐の髙さになっています。 つまり「体積」から計算できます。 その1で、「(1)この正三角錐の体積を求めなさい。」 を解説しており正四角錐の体積(底辺と高さから) 答えを知れて良かったが、途中式が分からないので、あまり勉強にはならなかった。 a=8,h=3にすると体積がになります。 (14桁の場合) 正しくは、64です。 修正お願いいたします。 失礼致しました。 ご指摘長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当な直交変換により、以下の方程式に変換できる。



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



毎日問題を解こう 11 苦手な数学を簡単に
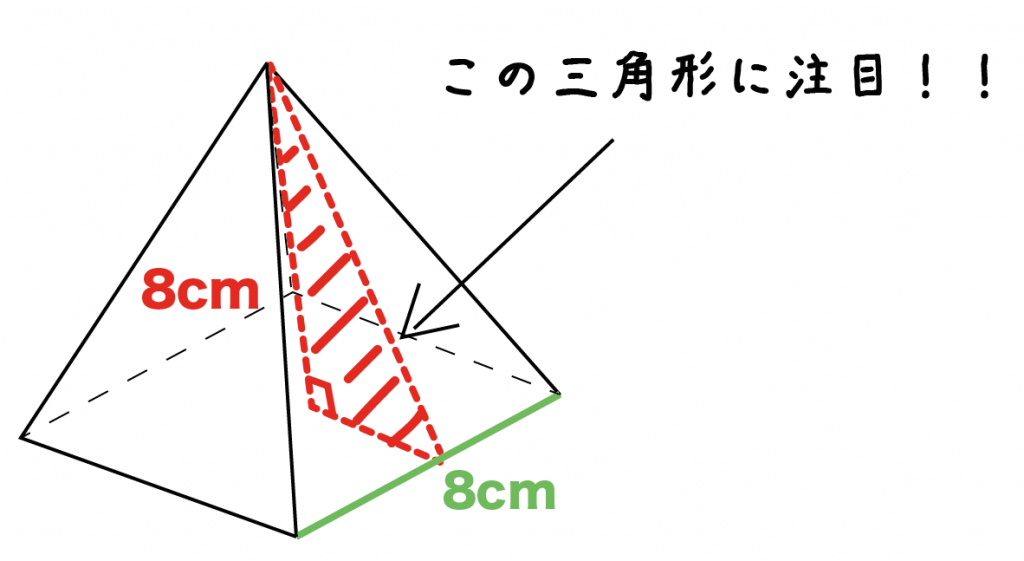
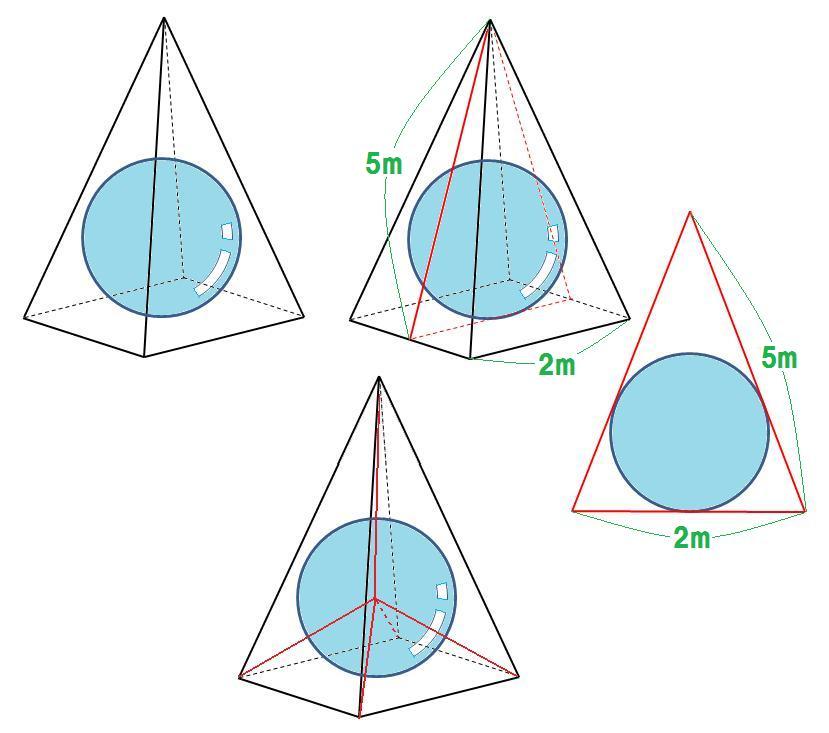
さらに、その半分の長さ まで求めておきましょう。 次に、正四角錐の高さを含む こちらの直角三角形に注目します。 すると、先ほど求めた ㎝ の辺を用いて 三平方の定理から高さを求めることができます。 ようやく正四角錐の高さが求まったのでこの縁は、 角錐の高さです。 にエッジabとsaが含まれる場合は、ピタゴラスの定理によって長方形のΔsabからの高さ sbを求めます。 これを行うには、正方形saから正方形abを引きます。 ルートを削除してください。正四角錐の体積の求め方\(2\)\(1\) 対角線と高さから正四角錐の体積を求めるときは、\(1\)番目に対角線の長さから正方形の面積を求めます。 対角線から正方形の面積を求める方法は次のとおり。 正方形




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




四角錐の体積の求め方 公式 小学生 中学生の勉強
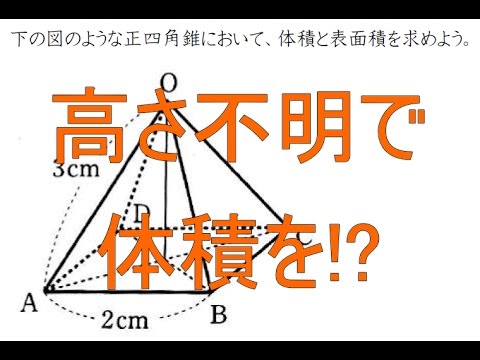
(例1)正四角錐OABCDが あります。底面ABCDは、 1辺の長さが6cmの正方 形で、ほかの辺の長さはすべ 色のついた部分の直角三角形を考えて高さhを三平方の定理から求めます。 h 2 =9 2 ー6 2 h 2 =45 h=3√5 体積=6 2 円すいの体積の公式 底面積×高さ×1/3 正四角錐の体積 底辺の1辺が6cm 他の辺が9cmの四角すいの体積を考えるAcは底面の正方形abcdの対角線なので ≫ 三平方の定理に当てはめて ac 2 =12 2 12 2 ac 2 =2 ac=±12 2 ac>0より ac=12 2 oからacに引いた垂線をomとすると これが四角錐の高さになる。 amはacの 1 2 なので am=6 2 ≫ o a c 15cm 15cm m 12 2 cm 6 2 cm oamで三平方の定理を使うと




正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学
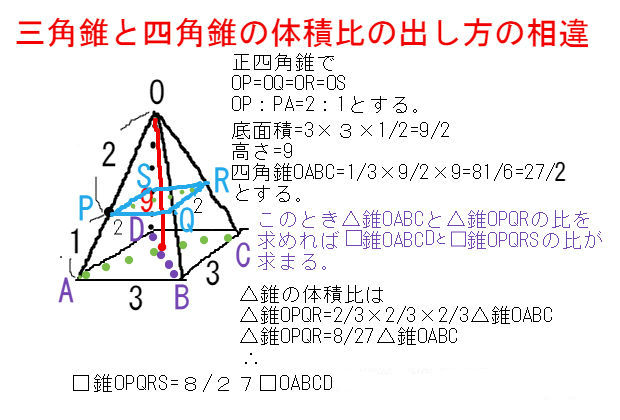



三角錐と四角錐の体積比計算方法の違い 中学 数学 理科の復習サイト
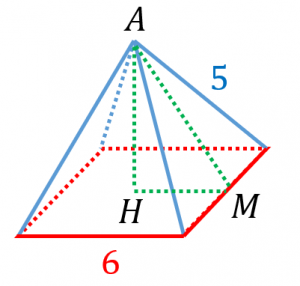
そのため、 高さは 。 面積は当然、底辺×高さ× で求められるので、以下の通りです。 = = こうした一般的な解き方でも1分以内に解答したいところですが、今回教える2大公式によって高さ2秒、面積3秒、合わせて5秒で答えを出すことができます。 そのすべての辺の長さが2 cm である正四角錐oabcd において,辺oc 上に中点e をとる。この正四角錐の 側面上に,頂点a から辺ob と交わり点e まで線をひ くとき,最も短くなるようにひいた線の長さを求めな さい。 類題 2 1 辺が6cm の正方形abcd について,辺bc正四角錐の体積の求め方\(1\)\(1\) 高さが分からない正四角錐の体積を求めるときは、\(1\)番目に直角三角形の比を使って、対角線の半分の長さを求めます。 \(\triangle{\mathrm{ABC}}\)は直角二等辺三角形なので、辺の比は\(11\sqrt{2}\)になります。 直角二等辺三角




四角錐高さ 求め方 角錐 円錐の體積と表面積の求め方 錐體の公式と母線 Otqz



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学
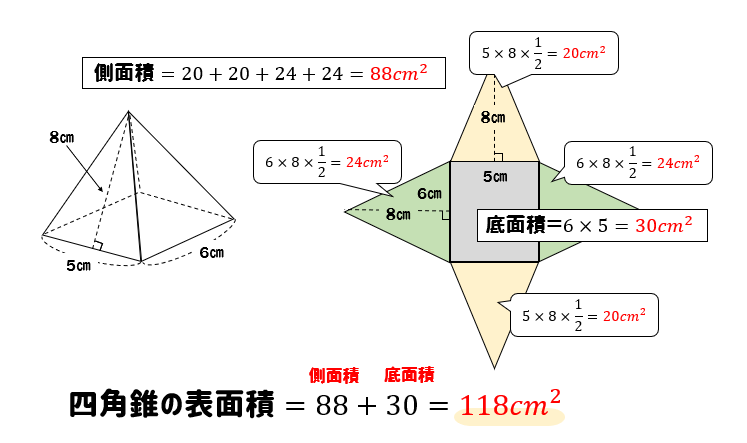
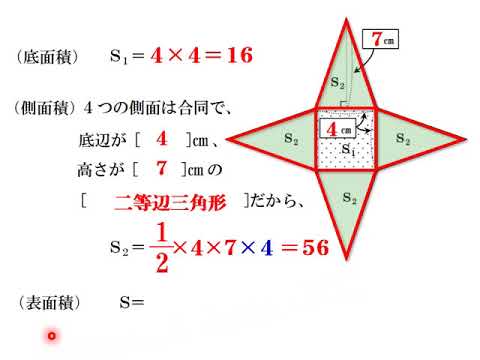
三角形の面積の求め方で側面積を出す → 縦×横×高さ÷2=底面積 四角錐の場合、側面は4つの三角形 扇形の面積の求め方で側面積を出す → 母線(もとの円の半径)×母線×円周率(π:314)×中心角の大きさ÷360=側面積 ←4 下の図の正四角錐の表面積を




中3数学 正四角錐の高さと体積 5分で学習 Youtube




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




四角錐の表面積の求め方 公式 小学生 中学生の勉強



正四角錐と三平方の定理 中学3年数学 Youtube



正四角錐の体積の求め方や高さの求め方などがわかりません教えてください Yahoo 知恵袋




表面積の求め方 計算公式一覧




正四面体の体積 高さが誰でも一発で求められるようになる 公式 展開図 高校生向け受験応援メディア 受験のミカタ



正四面体とは 高さ 体積 表面積の公式や求め方 受験辞典



Excelワークシート 正四角錐台の体積や表面積などを計算するワークシート 黒い箱の中




高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ




3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ



1
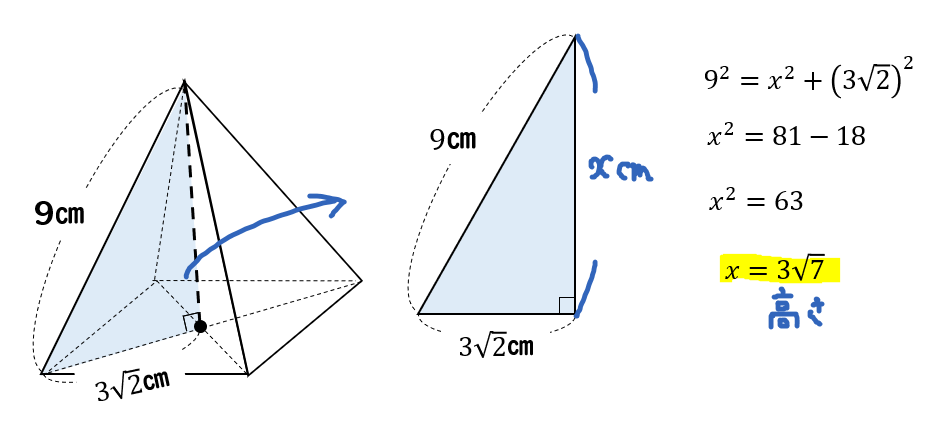



高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ
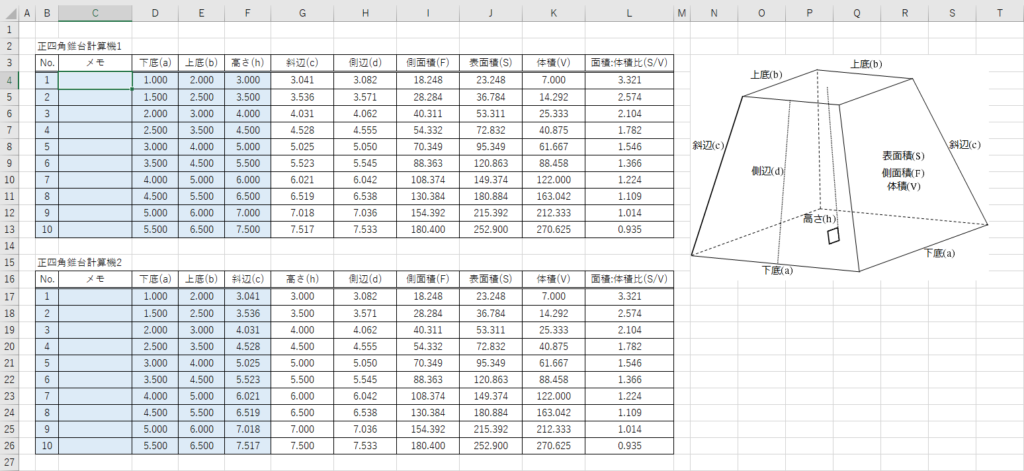



Excelワークシート 正四角錐台の体積や表面積などを計算するワークシート 黒い箱の中




四角錐の展開図の切り出し 名古屋市立大学14年 理系のための備忘録




四角錐の体積の求め方 公式 小学生 中学生の勉強
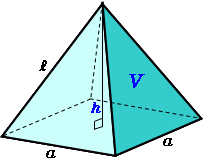



正四角錐の体積 底辺と側辺から 高精度計算サイト




三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント



正四角錐の高さ の求め方 至急お願いします 底面が一辺4cmの正方形で Yahoo 知恵袋



Mathematics 角錐の体積が角柱の3分の1になる証明 働きアリ




中3数学 正四角錐の高さの求め方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



正四角錐台の体積の求め方 Media Qikeru Yahoo 知恵袋




四角錐 Wikipedia




錐体の表面積1 例1正四角錐の表面積の求め方 Youtube



動画 正四角錐の表面積 Youtube




正四角錐 Geogebra



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学



答 正四角錐の内接球の半径 解答集




中3数学 正四角錐の高さの求め方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



この写真の正四角錐の高さの求め方教えてください 四角錐の体積の公式 Yahoo 知恵袋




中3数学 正四角錐の高さの求め方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



高校数学 正四面体 高さ 体積 オンライン無料塾 ターンナップ Youtube



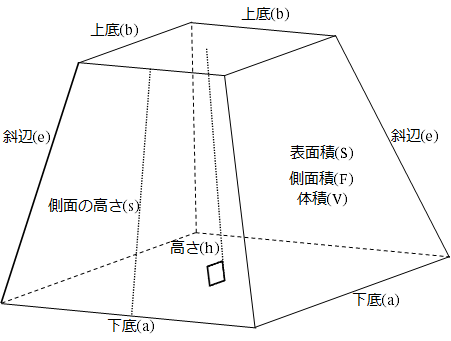
四角錐台の公式 体積 側面積 表面積 数学 エクセルマニア
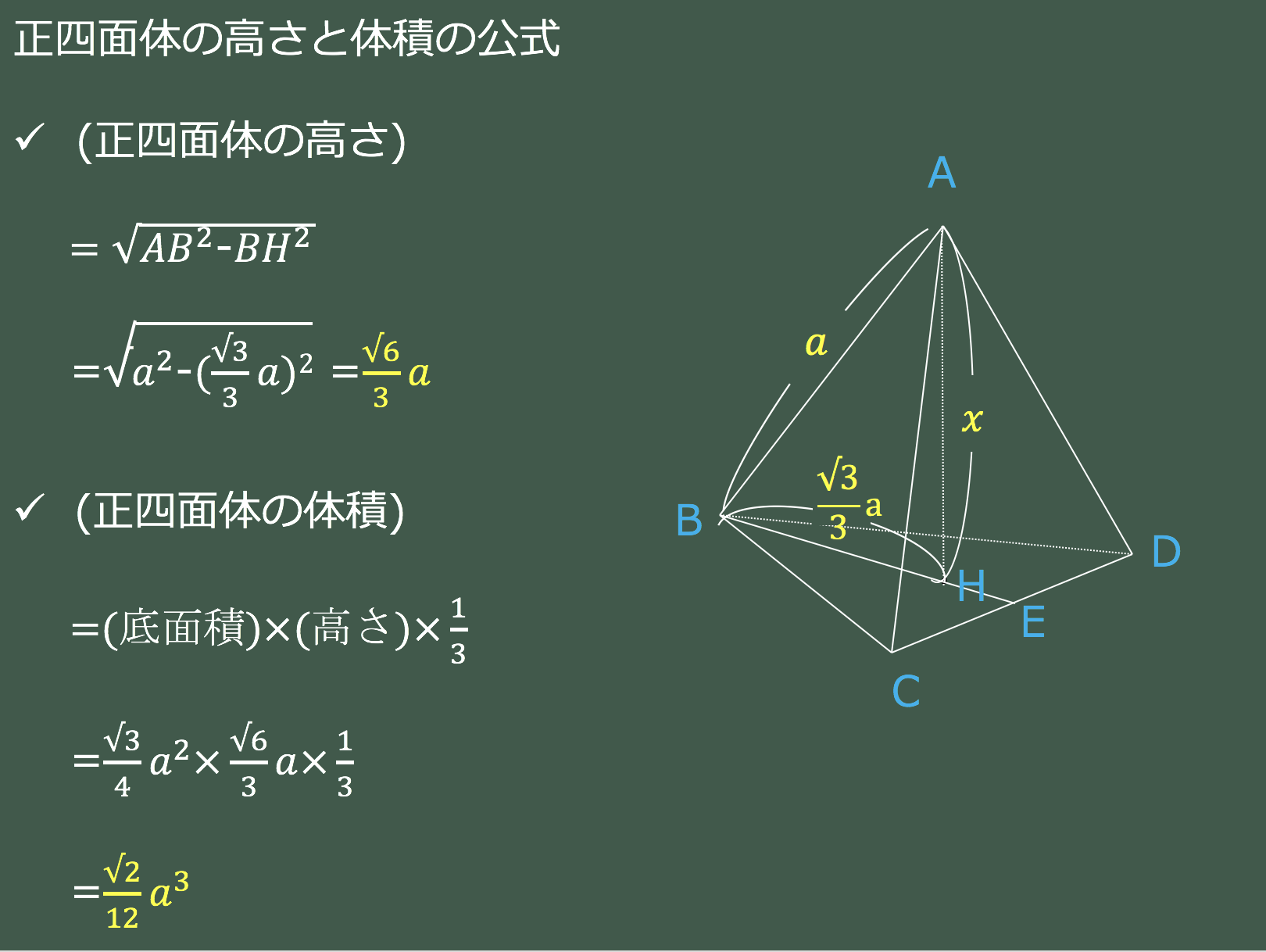



3分で分かる 正四面体の高さ 体積の求め方をわかりやすく 合格サプリ



三角錐とは 体積 表面積の公式や求め方をわかりやすく解説 受験辞典
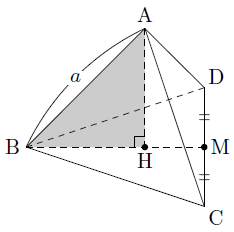



角錐の高さと体積 まなびの学園




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




数学 B 最大値と最小値に関する文章題 金城学院大 学習院大 大学入試数学の考え方と解法




四角錐の表面積の出し方 また 質問します まちゅといいます 図のよう Okwave




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




どうして1 3なの 錐の体積の公式の求め方 まなべーと
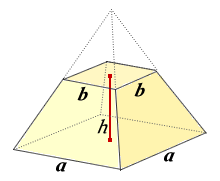



みんなの知識 ちょっと便利帳 正四角錐台の側面積を計算する
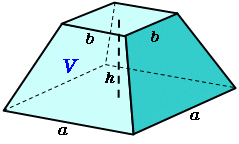



正四角錐台の体積 高精度計算サイト
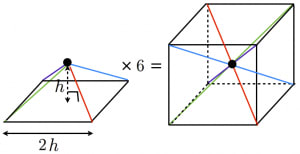



錐体の体積に1 3がつくことの2通りの説明 高校数学の美しい物語




2 が分かりません Clearnote




この問題で 解説の 1 高さ4cmとありますが 2 の解説では 高さ Oh Clearnote
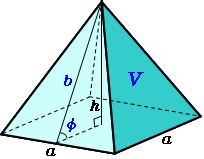



正四角錐の体積 底辺と高さから 高精度計算サイト




角錐 円錐の体積と表面積の公式 数学fun
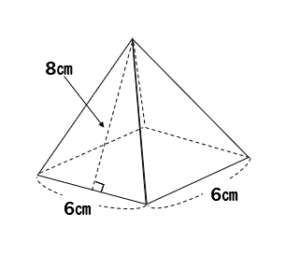



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




至急お願いします 中3数学です 正四角錐の投影図から体積を求める問題です Clearnote




四角錐公式 Mdsulja
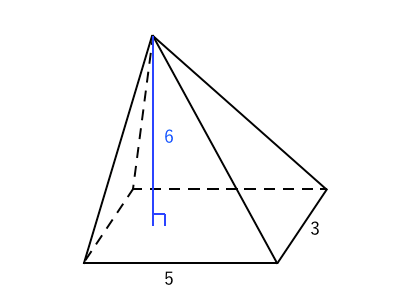



超簡単 体積の求め方 苦手な数学を簡単に




四角錐高さ 求め方 角錐 円錐の體積と表面積の求め方 錐體の公式と母線 Otqz
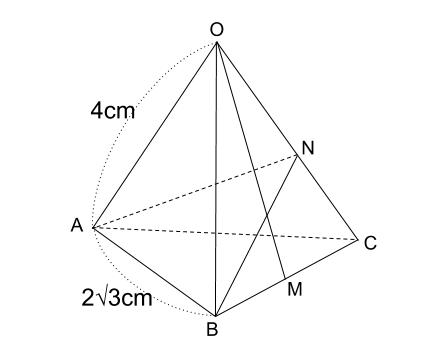



正四角錐の良問 その1 中学数学の無料オンライン学習サイトchu Su



第360問の解答




四角錐の表面積の求め方 公式 小学生 中学生の勉強



1
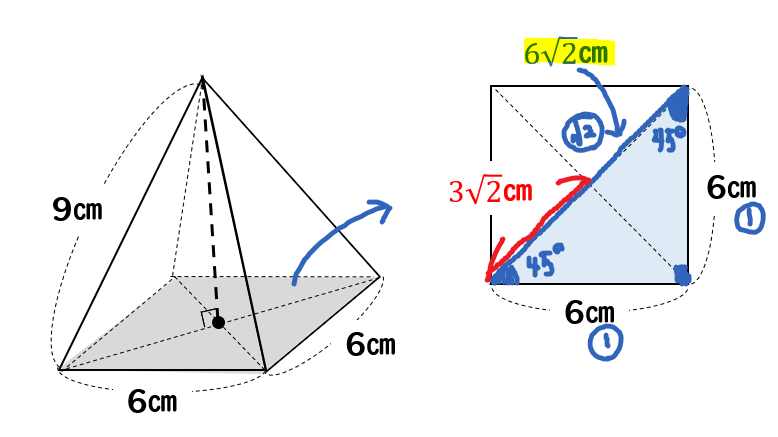



高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ




四角錐公式 Mdsulja




正四角錐の外接球 数学カフェjr




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
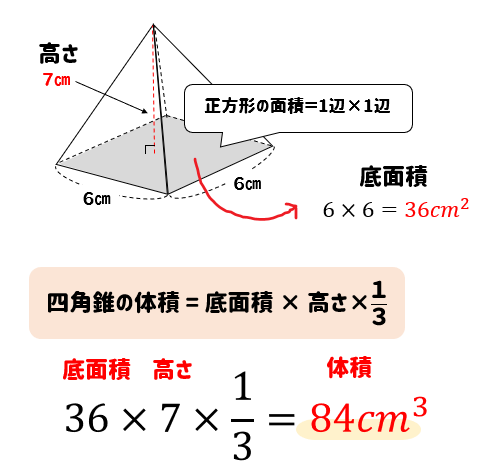



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




塾 学校 家庭を結ぶ 受験情報サイト 学びネット
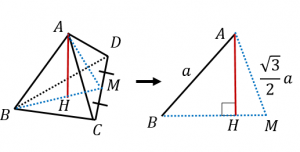



正四面体の高さと体積の求め方 具体例で学ぶ数学



図は側面が正三角形の正四角錐である 一辺の長さは6 である 1 体積を求 Yahoo 知恵袋




四角錐の体積の求め方 公式 小学生 中学生の勉強




この正四角錐の高さの求め方をおしえてください Clearnote



3



Excel関数 正四角錐 ピラミッド型 の体積や表面積を計算するrsqpyramidカスタムワークシート関数群 黒い箱の中




三平方の定理の利用 四角錐 円錐 チーム エン




四角錐高さ 求め方 角錐 円錐の體積と表面積の求め方 錐體の公式と母線 Otqz




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun
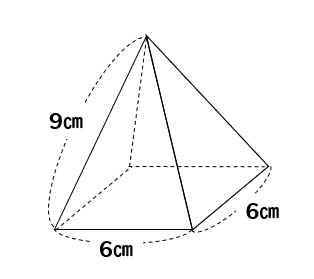



高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ




四角錐 Wikipedia




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




高校入試対策数学 空間図形問題 正四角錐 体積 三平方の定理 特別な直角三角形 二方面シリーズ 面積 Youtube




正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ



1
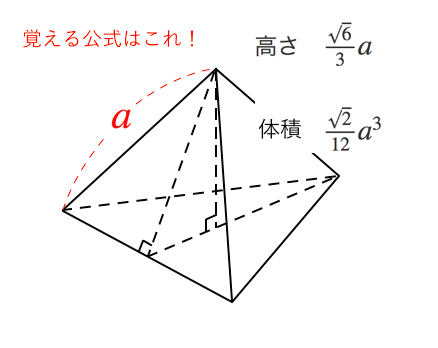



正四面体 高さ 面積を求める公式 苦手な数学を簡単に




考えてもやり方が分かりませんでした 教えてほしいです Clearnote




中3数学 正四角錐の高さの求め方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく




四角錐高さ 求め方 角錐 円錐の體積と表面積の求め方 錐體の公式と母線 Otqz




数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



Studydoctor正四角錐と三平方の定理 中学3年数学 Studydoctor




なぜ 錐体 は3で割る 簡単な説明を 正多面体 から伝授します 横山 明日希 ブルーバックス 講談社 3 4
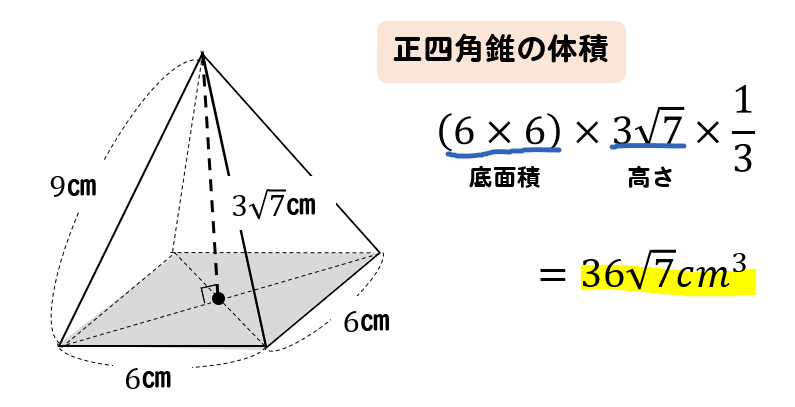



四角錐高さ 求め方 Phantom Public
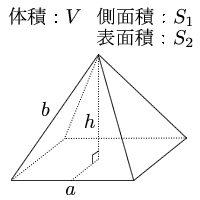



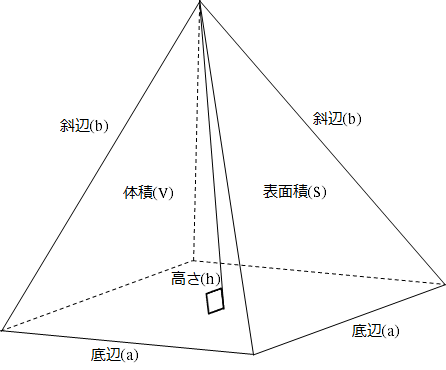
正四角錐 底辺と斜辺 体積 表面積の計算 計算サイト




四角錐台の体積 高精度計算サイト



下のような四角錐台の体積の求め方をわかりやすく教えてください A 5b 3 Yahoo 知恵袋




四角錐の表面積の求め方 公式 小学生 中学生の勉強




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
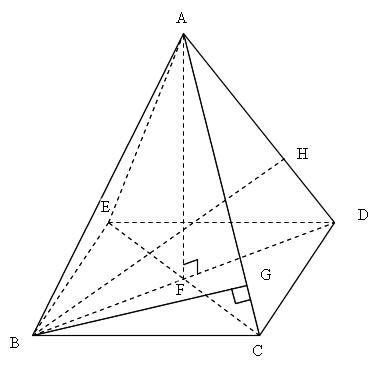



Mathematics 空間図形 四角錐 大阪府公立 21年前期理数科 働きアリ
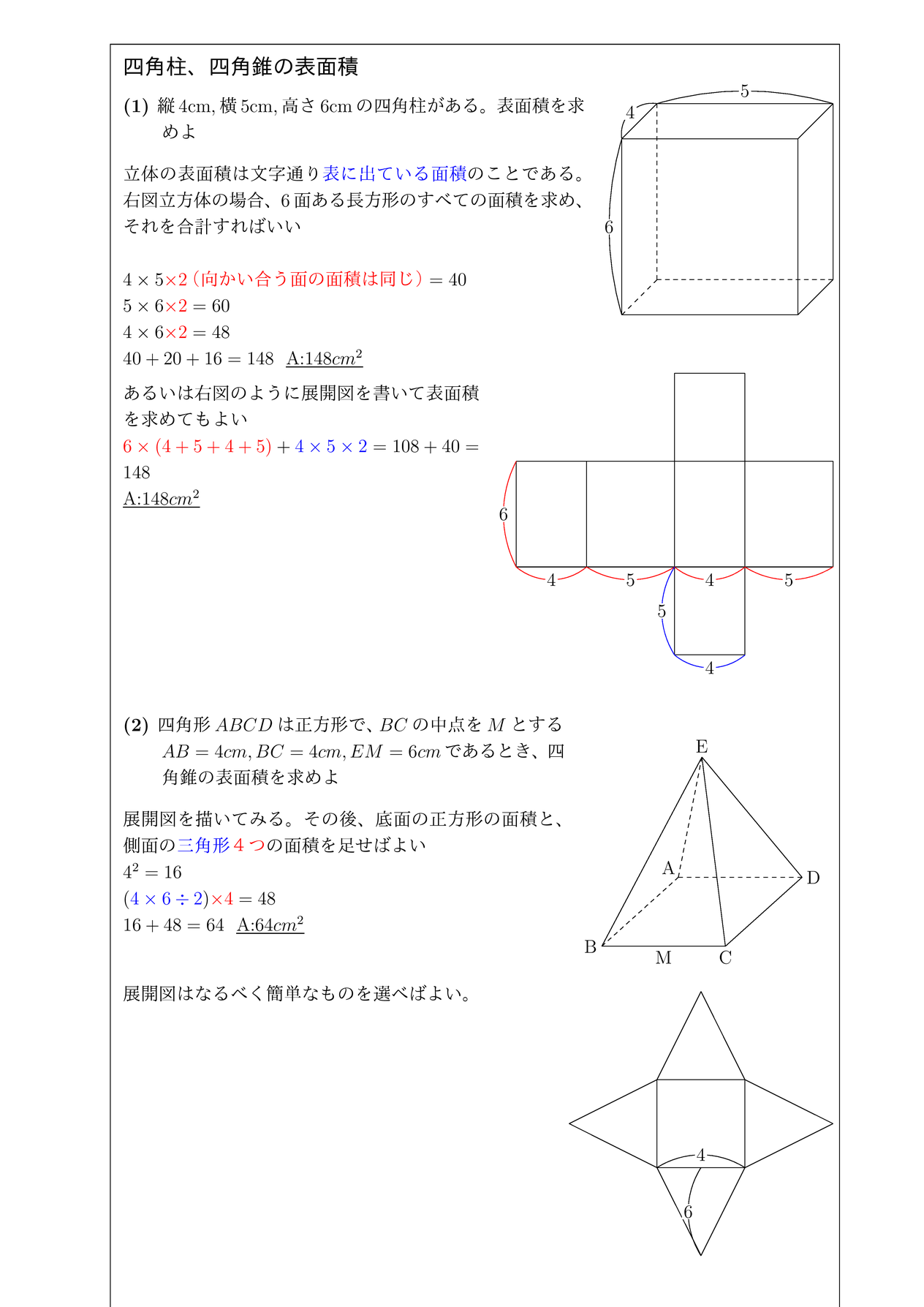



四角柱 四角錐の表面積 チーム エン




わかる方教えてください Clearnote
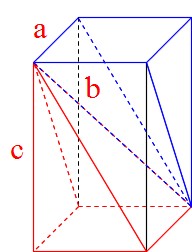



Mathematics 角錐の体積が角柱の3分の1になる証明 働きアリ



角錐台の体積 高精度計算サイト


