++ 50 ++ 三角形 の 相似 条件 証明 180886
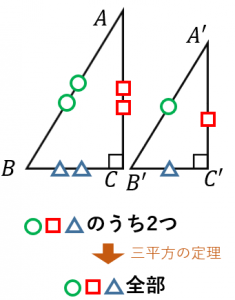
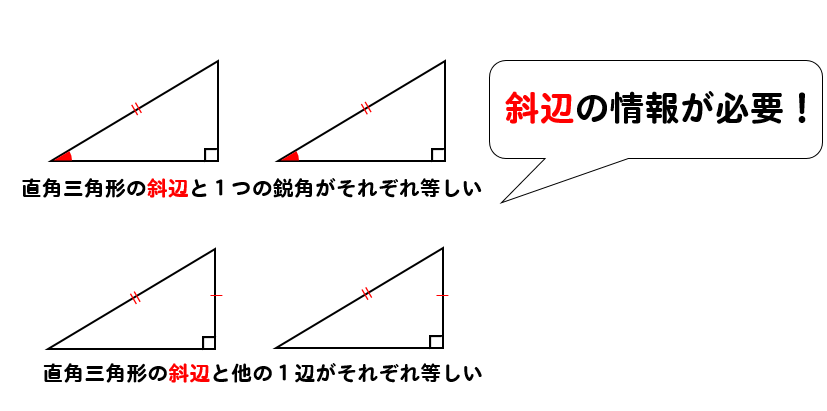
相似というのは、おおざっぱにいえば「形は同じで大きさが違う」ものを言うので Lesson 31 三角形の相似条件と証明 第5章 図形と相似 <前:L30 三角形の相似条件 の問題 L31 三角形の相似条件と証明 の解答:次> 練習問題1 以下の1~3に示した各組の・相似の性質 ・三角形の相似 ・三角形の相似の証明 ・空間図形の相似 ・相似の練習問題 を見てきました。 本記事の目的は相似のイメージを掴むことです。 この記事を読んで相似の基礎を理解した後、最後に相似を完璧にするのはあなた自身です。直角三角形の合同条件 ① 直角三角形の斜辺と $\textcolor{blue}{1}$ つの鋭角がそれぞれ等しい ② 直角三角形の斜辺と他の $\textcolor{blue}{1}$ 辺がそれぞれ等しい どちらの条件も「直角と斜辺は等しい」ので、違いは $1$ カ所だけになります。

三角形の相似条件と証明問題の解き方 数学fun
三角形 の 相似 条件 証明
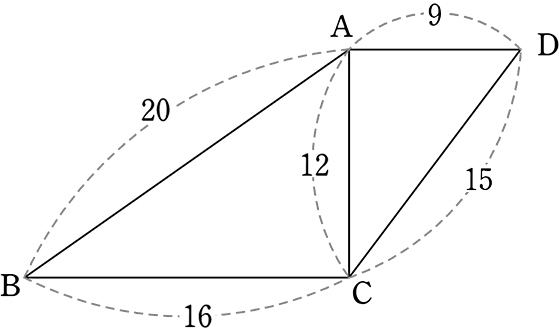
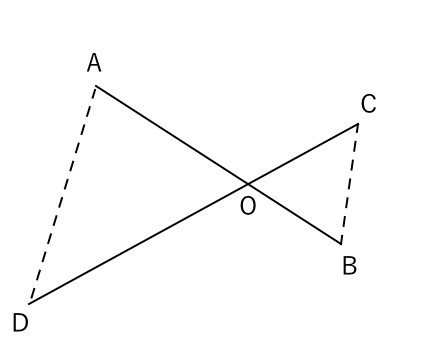
三角形 の 相似 条件 証明-三角形の「合同条件」と「相似条件」 を勉強してきたよね。 両方とも 数学の証明 のために必要なアイテムだから、テスト前には覚えなきゃいけないね。3 相似条件と証明 三角形の相似条件を使って,図形の性質を証明する 例1.四角形abcd で,点o はac,bd の交点です。 このとき, oad ∽ ocb であることを証明しなさい。 また,bc の長さを求めなさい。 oad と ocb において ao:co =3:6 =1:2
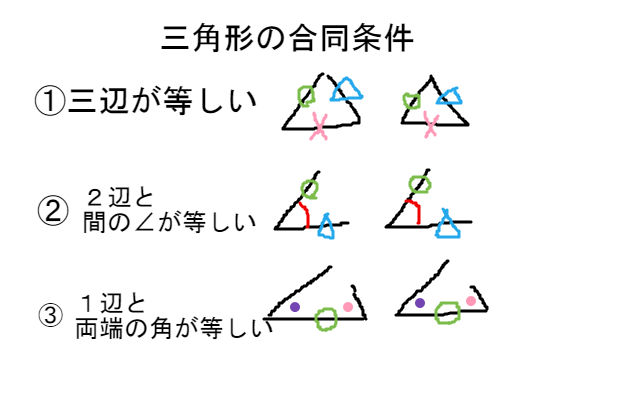


三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト
証明したいことを図(自作)に印づける。 問題文から証明に使えそうなヒントを図に書き入れる。 合同条件(または相似条件)の3つからどれが当てはまるかを探る。 条件が揃わない場合は、 図から判断して条件に当てはまりそうなところが無いかを探る。相似な図形/三角形の相似条件/相似の証明:2 辺の比とその間の角/2 組の角が等しい/ 直角三角形など /三角形の相似と長さ/FdData 中間期末製品版のご案内 FdData 中間期末ホームページ 掲載のpdf ファイル(サンプル)一覧4 三角形の相似条件の証明の仕方 5 三角形の相似条件を満たすと、なぜ相似になるのですか。 6 図のように正六角形をその中心で通る対角線で区切り、6個の合同な正三角形に分ける。これら6個の三角形を 7 中学2年生で覚える三角形の合同条件を使った証明
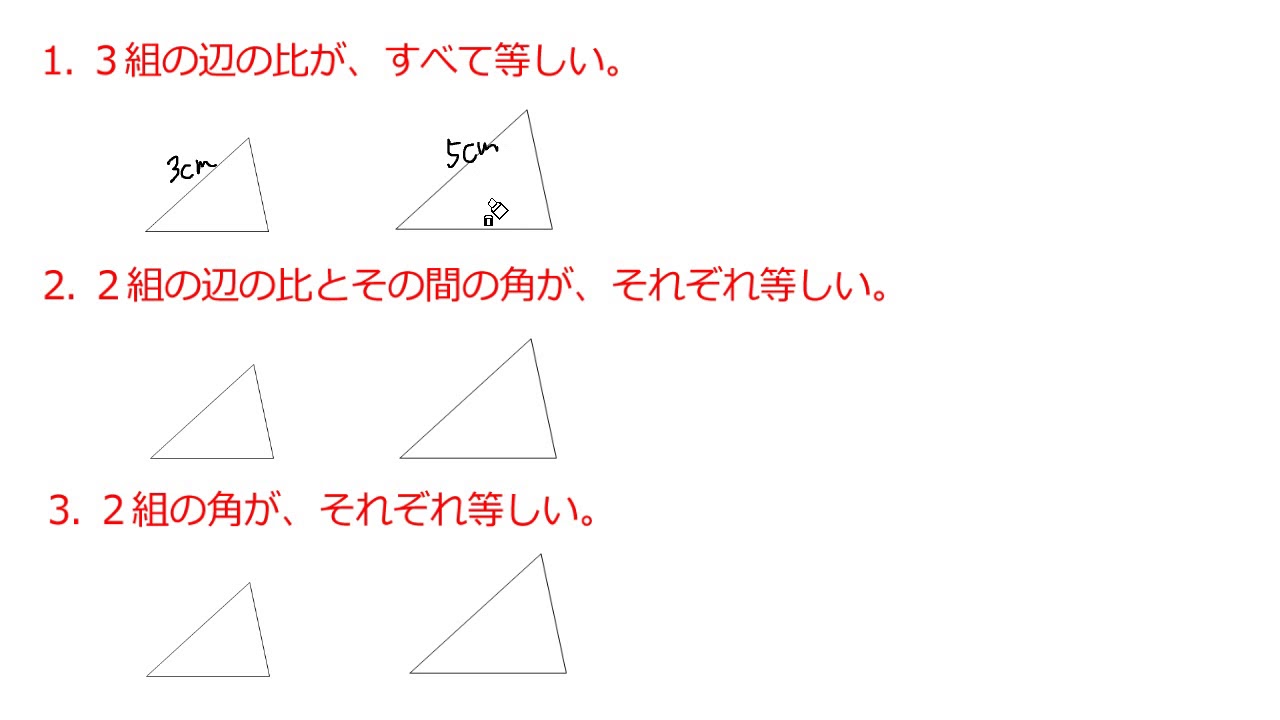
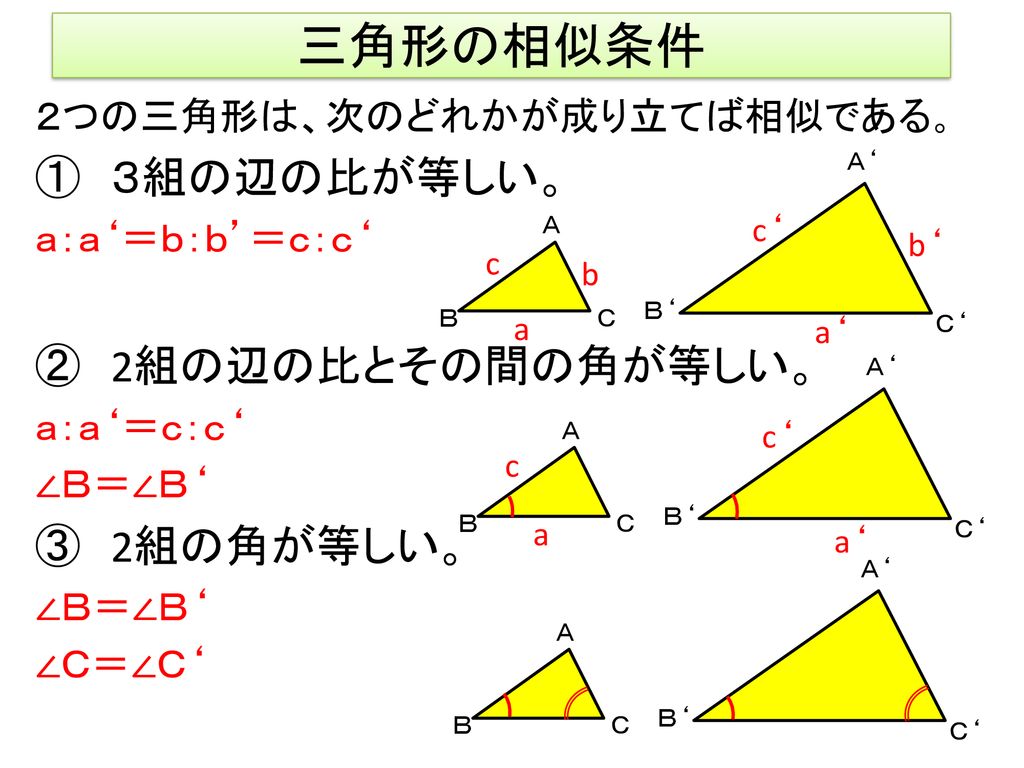
命題6ー31(直角三角形の辺上の相似な図形) 直角三角形において 直角に対する辺の上の図形は 直角をはさむ2辺の上の 相似でかつ相似な位置に描かれた 図形の和に等しい。 直角三角形は、 定義1ー21 による。 直角は、 定義1ー10 による。「図形の中から相似な三角形を見出し、相似条件を用いて証明することができる。 2つの三角形は、次のどれかが成り立てば相似である。 ① 3組の辺の比が等しい。直角三角形の合同条件 ① 直角三角形の斜辺と $\textcolor{blue}{1}$ つの鋭角がそれぞれ等しい ② 直角三角形の斜辺と他の $\textcolor{blue}{1}$ 辺がそれぞれ等しい どちらの条件も「直角と斜辺は等しい」ので、違いは $1$ カ所だけになります。
や三角形の相似条件を用いて証明する。(7) 理したことの間のつながりを考える。 ・証明としての形式的な表現等にとらわ 第三次 相似な図形の相似比と面積比及び体積比と れず,日常言語に近い形で確認するよ それらの関係について考える。(2) うにする。証明したいことを図(自作)に印づける。 問題文から証明に使えそうなヒントを図に書き入れる。 合同条件(または相似条件)の3つからどれが当てはまるかを探る。 条件が揃わない場合は、 図から判断して条件に当てはまりそうなところが無いかを探る。三角形の相似の証明 (木) 三角形の相似条件には,「対応する3組の辺の比がすべて等しい」「対応する2組の辺の比が等しく,その挟む角が等しい」「対応する2組の角がそれぞれ等しい」の3つがあるが,定期テストや高校入試で出される問題では


相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット
三角形の相似の証明 中学2年で学習した、三角形の合同の証明とほぼ同じです。 用いるのが合同条件ではなくて、相似条件になっただけです。 三角形の合同の証明があやふやな人は、そこから学習をしましょう。 急がば回れです。 証明の手順 証明の手順は「合同の証明のときと同様です数学・算数 三角形の相似条件 「2つの三角形の対応する3辺がそれぞれ平行ならば、両三角形は相似である」 求値問題においてこの相似条件を証明なしで使うと減点になりますか? 質問No965動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru



高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月



無料 中3数学 基本問題 解答プリント 図形の相似2 相似条件と証明
Lesson 30 三角形の相似条件 第5章 図形と相似 <前:L30 三角形の相似条件 の問題 L31 三角形の相似条件と照明 の問題:次> 練習問題1 以下の1~3の各組の三角形は相似である。 このとき、それぞれの相似条件を答えなさい。こんにちは、ウチダショウマです。 今日は、中学2年生で習う関門 「三角形の合同条件」 について、まずは図形の合同を確認し、次に合同条件を用いる証明問題を解き、またコラム的な内容も考察していきます。 コラム的な内容としては 目次4「作図を先に習う理由」目次2「3つの合同条件は「二等辺三角形の作図から証明を使って性質を導くことができる。 「定義や定理の用語の意味を理解する。 下の図で、点Aを中心にして直線ℓと交わる円をかき、その交点をB,Cとして、 ABCをかきましょう。
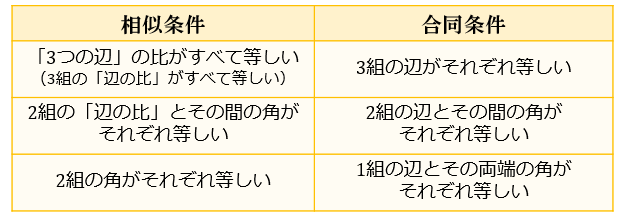


三角形の合同条件 相似条件と合同条件の違いとは アタリマエ
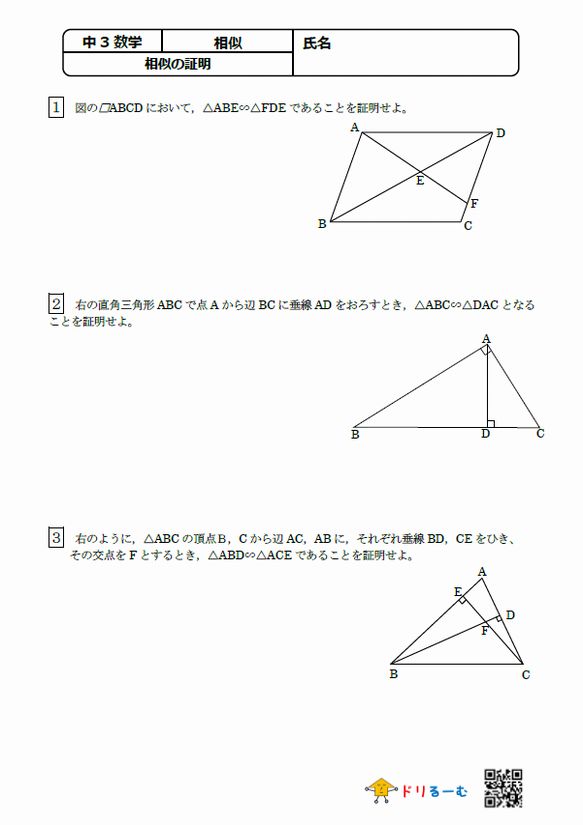


三角形の相似条件 ドリるーむ
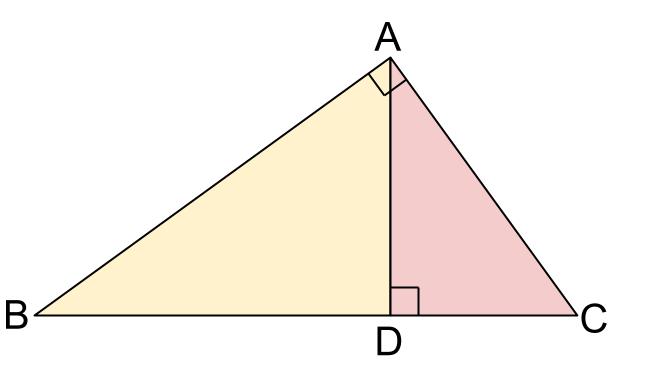
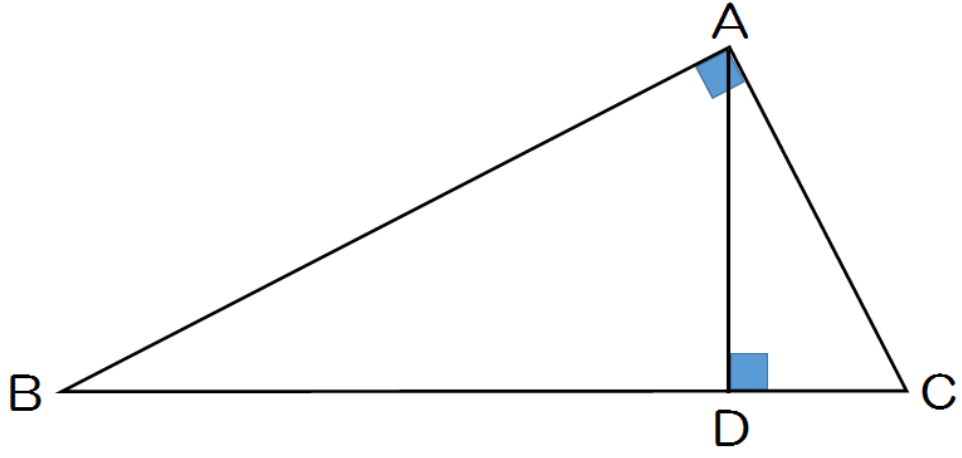
相似というのは、おおざっぱにいえば「形は同じで大きさが違う」ものを言うので Lesson 31 三角形の相似条件と証明 第5章 図形と相似 <前:L30 三角形の相似条件 の問題 L31 三角形の相似条件と証明 の解答:次> 練習問題1 以下の1~3に示した各組の図の abcは∠bac=90°の直角三角形である。頂点aから辺bcに垂線を下ろしその交点をdとする。 a b c d abd∽ cbaを証明せよ。三角形の相似条件 \(2\) つの三角形があり、それらが相似であるかどうかを判定する。 そのために、三角形の相似条件があります。 相似条件 \(3\) 組の辺の比がそれぞれ等しい \(2\) 組の辺の比とその間の角がそれぞれ等しい \(2\) 組の角がそれぞれ等しい 三角形の合同条件というものを、中学 \(2\)



保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく



中学数学 学研教育出版 牧野正博著 三角形の相似条件を利用した証明 2 P 418 113 Mathtriangleの雑記帳
こんにちは、ウチダショウマです。 今日は、中学3年生で習う 「三角形の相似条件」 について、まずは図形の相似を解説し、次に三角形の相似条件が $3$ つである理由を明らかにしていきます。 また記事の後半では、狙われやすい証明問題をいくつか用意しましたので、ぜひチャレンジしてみ



相似の証明です 答えは写真の通りだったのですが 私の答えで 中学数学に関する質問 勉強質問サイト
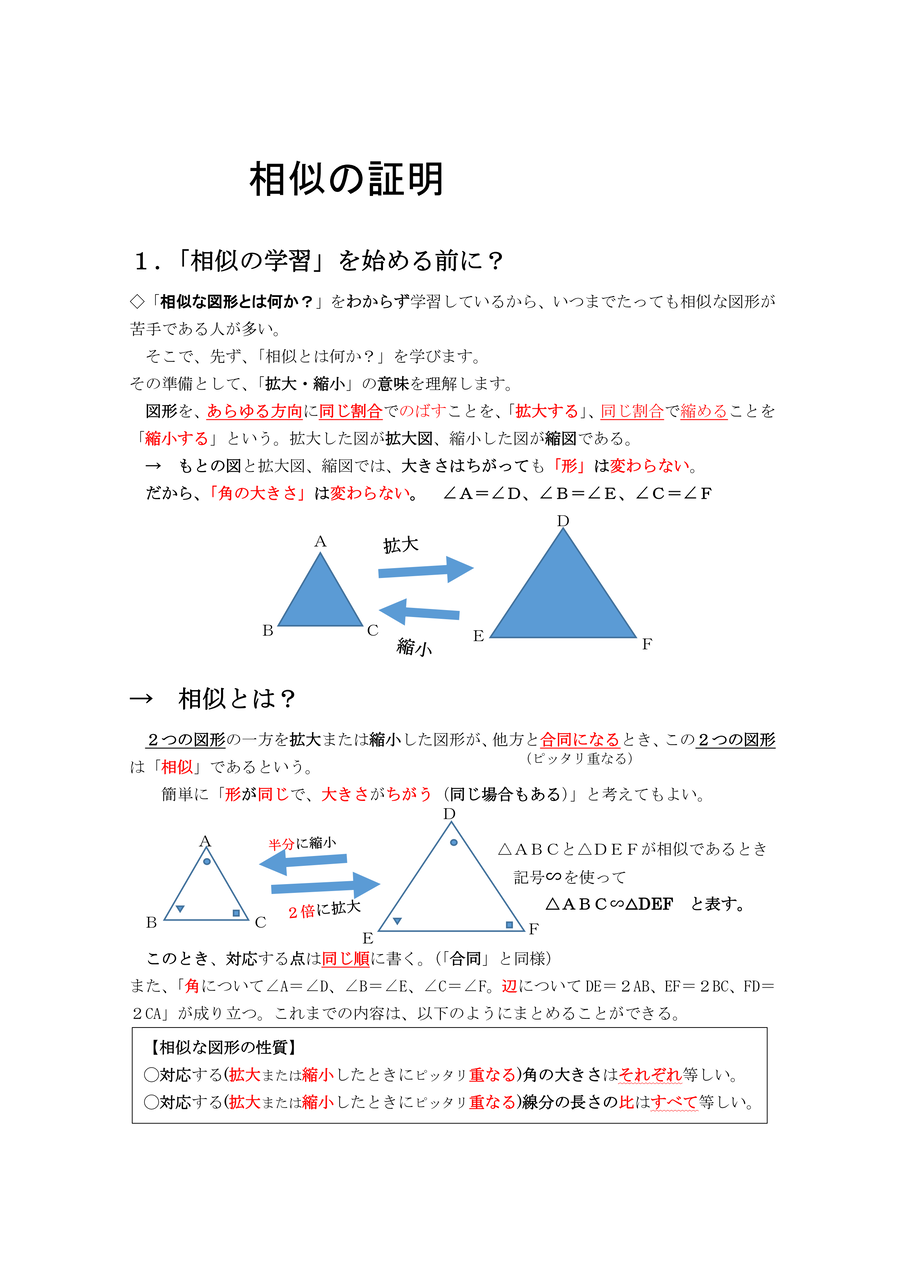


中学校数学 証明のコツ 相似


Studydoctor三角形の相似条件 中3数学 Studydoctor



三角形の相似条件
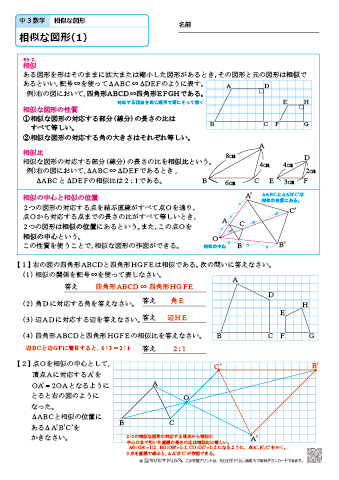


中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学



三角形の相似条件と証明問題の解き方 数学fun



世界一わかりやすい数学問題集中3 5章 図形と相似
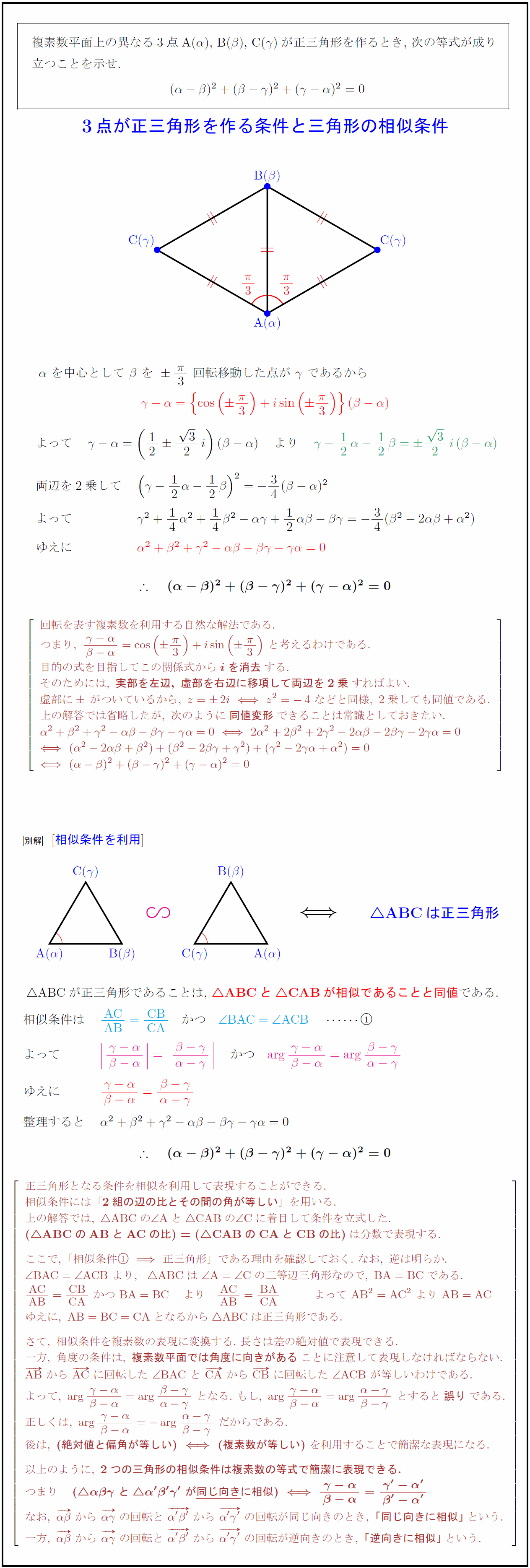


高校数学 複素数平面上で3点が正三角形を作る条件と三角形の相似条件 受験の月



三角形の相似条件と基本的な証明 無料で使える中学学習プリント
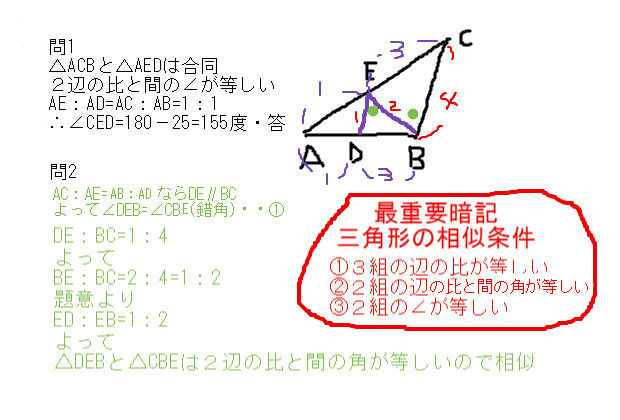


おしゃれな 相似 の 証明 壁紙 配布



令和3 21 年度用 中学校数学 内容解説資料a
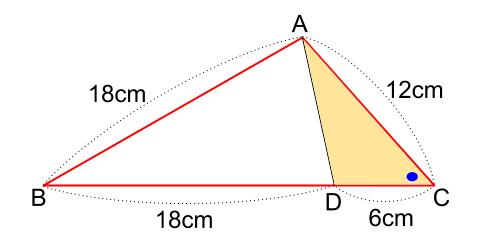


中学数学 相似の証明 その1 中学数学の無料オンライン学習サイトchu Su


Math 相似 直角三角形 正三角形と相似 働きアリ


三角形の相似条件 修正 Youtube


直角三角形の相似条件 具体例で学ぶ数学


受験数学かずスクール 三角形の合同条件と直角三角形の合同条件と三角形の相似条件



中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット



数学a 図形の性質 以下の問題の解説赤線部について 相似条件は 3辺が等しい Clear



三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
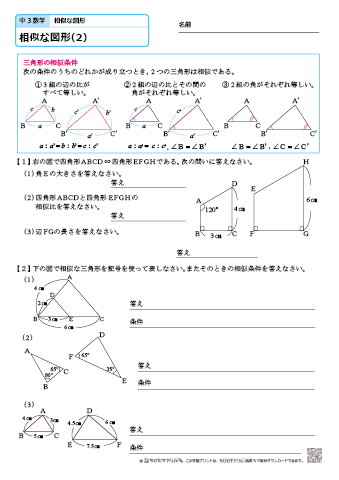


中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
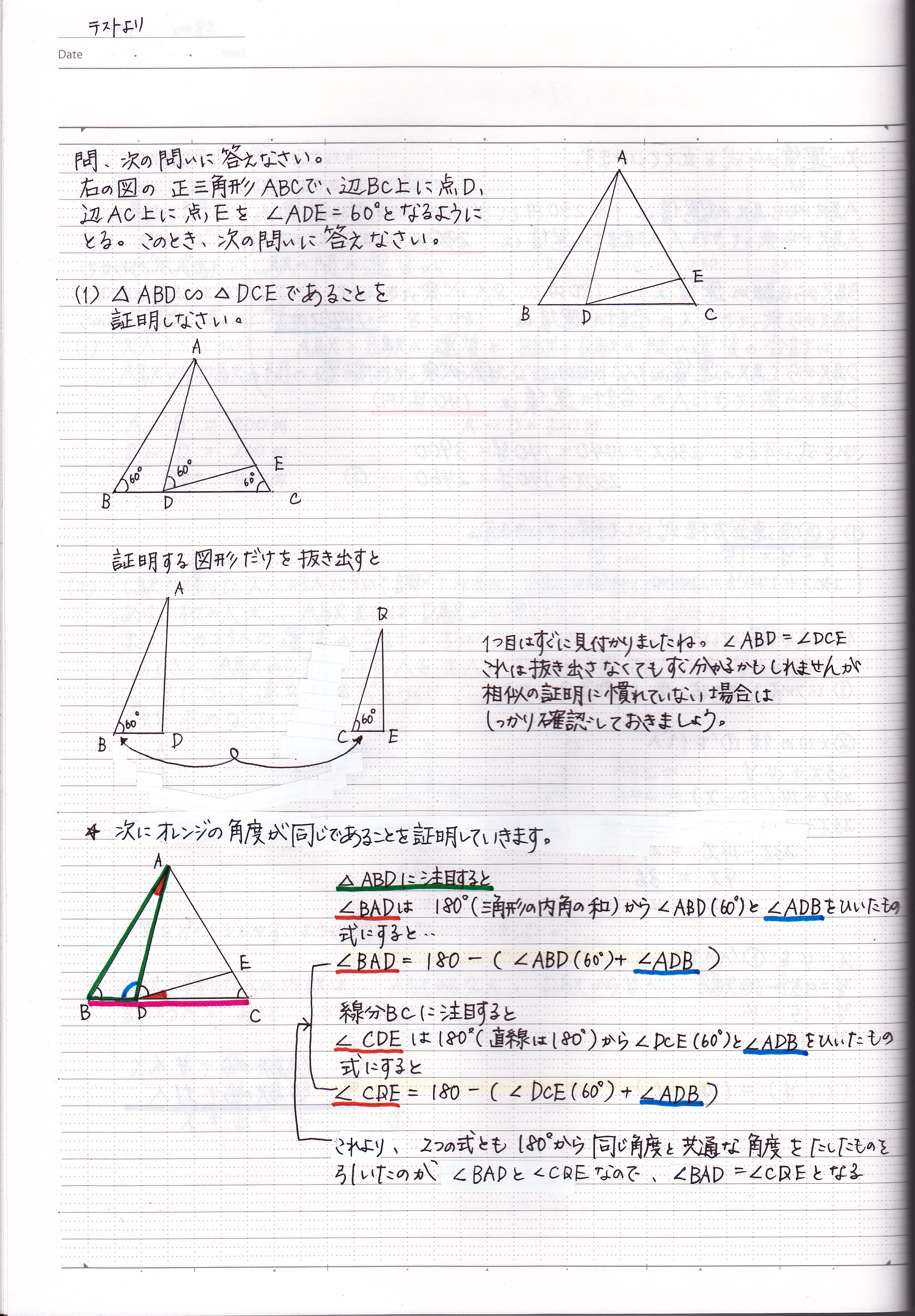


三角形の相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方
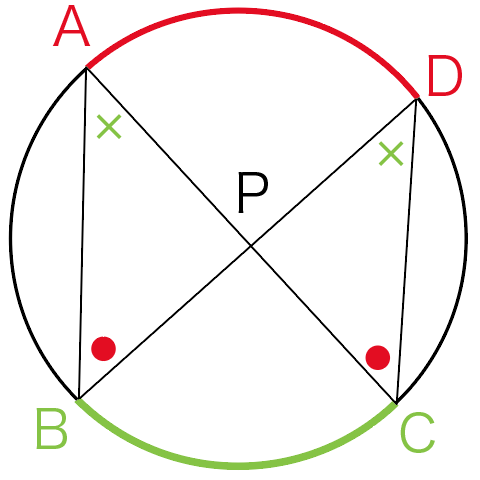


円周角の定理をつかった証明問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



三角形の相似条件と基本的な証明 無料で使える中学学習プリント



世界一わかりやすい数学問題集中3 5章 図形と相似



この3問がどうしても わかりません 回答お願いいたします もしよければ途中経過も Clear



無料 中3数学 標準問題 解答プリント 327 図形の相似2 相似条件と証明


合同条件 合同生效条件 合同终止条件 合同解除条件



数学 中3 46 相似の証明チャレンジ Lv 1 Youtube



中3数学 相似 直角三角形と相似 Youtube


三角形の相似の証明 平行線の錯角 勉強ナビゲーター
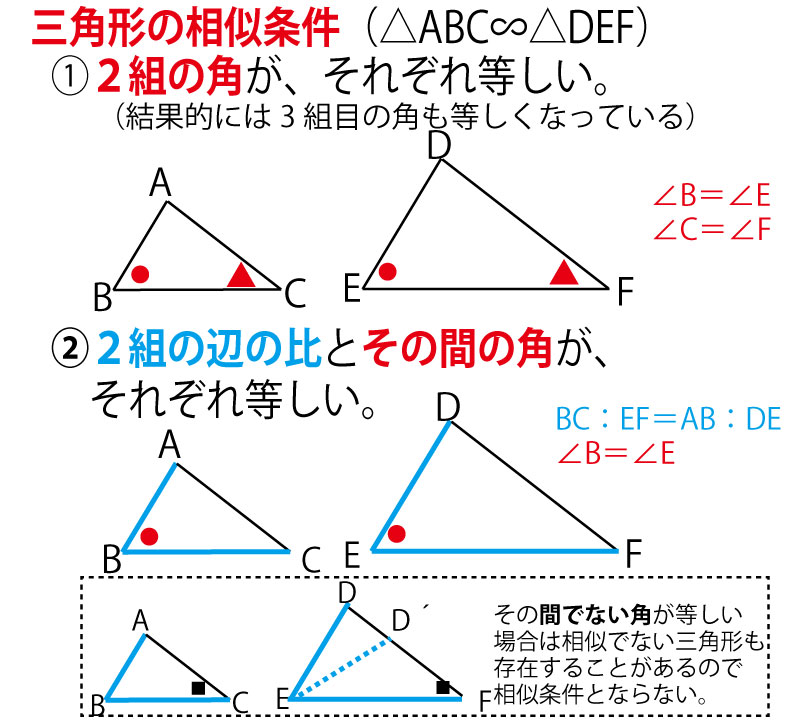


19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト


Studydoctor正三角形と相似の証明 中3数学 Studydoctor


数aの証明がわからないです 証明の2行目は平行であることからな Yahoo 知恵袋
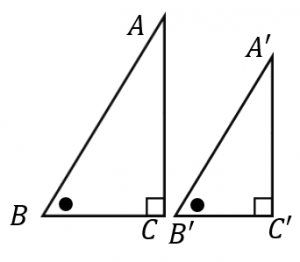


直角三角形の相似条件 具体例で学ぶ数学


中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su


中学数学 図形の相似



5章1節2 三角形の相似条件2 数学のすすめ


図形と証明 相似 スタディーx



三角形の相似条件



三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト



3年ー5章ー図形と相似 ワカデキな中学校数学



相似の証明 チーム エン


三角形の相似条件と有名な例題3問 具体例で学ぶ数学


数学 相似条件と証明 について 下の図 写真 で Abcは Ab Yahoo 知恵袋



中3 相似 証明問題について Okwave



中学数学 図形の相似
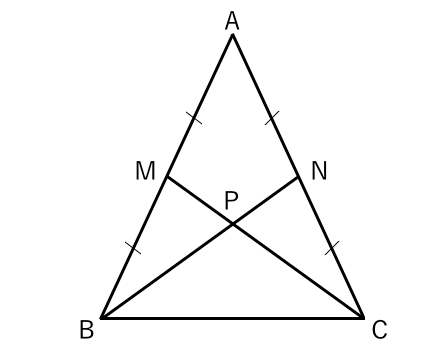


合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に


相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス


栃木県総合教育センター 算数 数学 学びの杜 中学校3年生 数学 三角形の相似条件と証明



三角形の相似条件
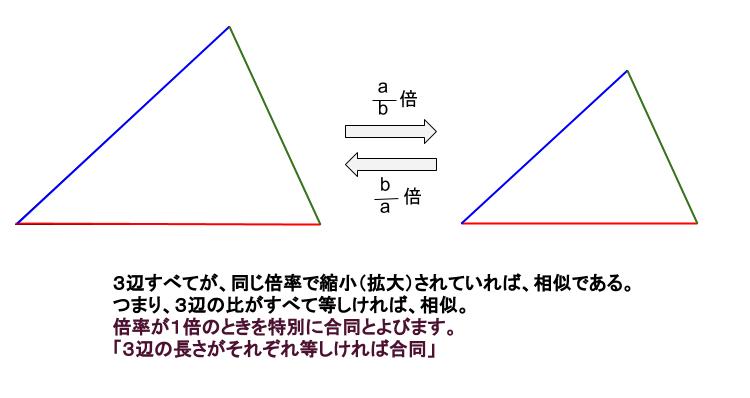


中学数学 三角形の相似条件 中学数学の無料オンライン学習サイトchu Su
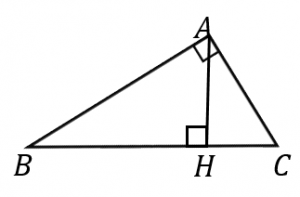


直角三角形の相似条件 具体例で学ぶ数学



5章1節2 三角形の相似条件2 数学のすすめ
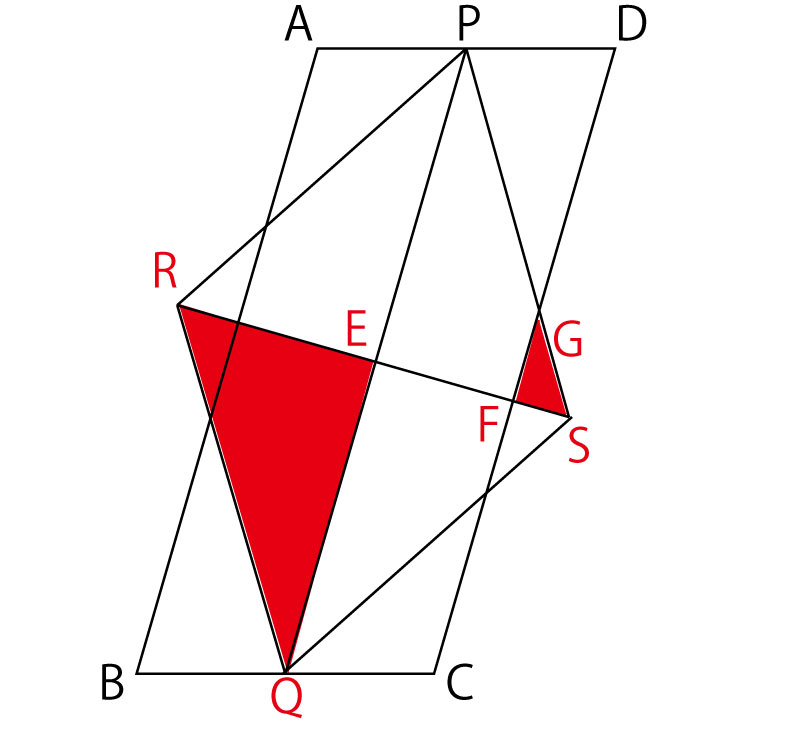


19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト


相似の証明 2つの正三角形と共通な角 勉強ナビゲーター


相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
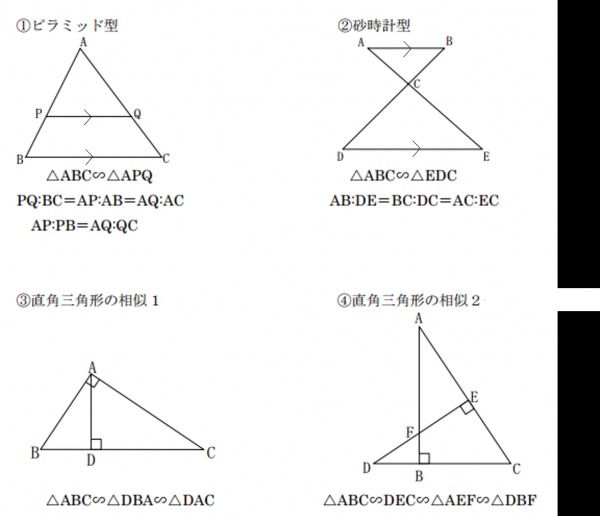


三角形の相似 合同条件 優技録
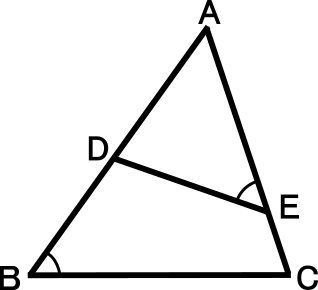


中学3年数学練習問題 三角形の相似条件と証明の問題



円周角を使った三角形の相似条件 現役医師による難関高校受験塾 Core コア



17年10月30日 数学 三角形の相似条件 オンライン家庭教師 ウェブリー



三平方の定理の証明 相似な三角形を使う方法 数学教材


相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



三角形の相似条件 相似な三角形の対応する辺の比は 相似比に等 中学数学に関する質問 勉強質問サイト
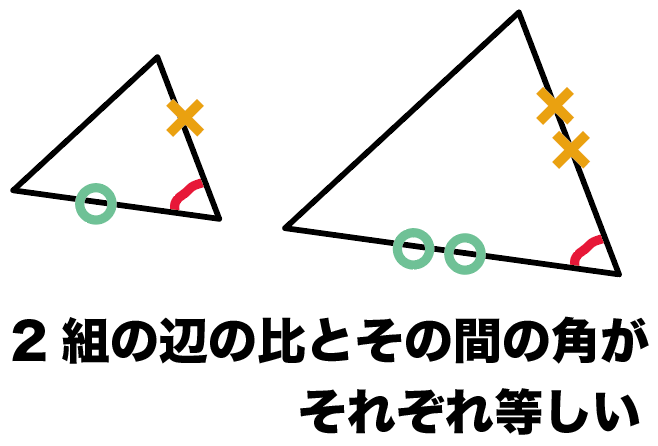


2分でわかる 三角形の3つの相似条件 Qikeru 学びを楽しくわかりやすく



三角形の合同条件と証明問題の解き方 数学fun



Ppt 相似条件と証明 Powerpoint Presentation Free Download Id



三角形の合同条件 相似条件と合同条件の違いとは アタリマエ



直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題



中学3年数学 相似条件を使った証明 2学期期末テスト 赤城



三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題



数学 中3 48 相似の証明チャレンジ Lv 3 Youtube
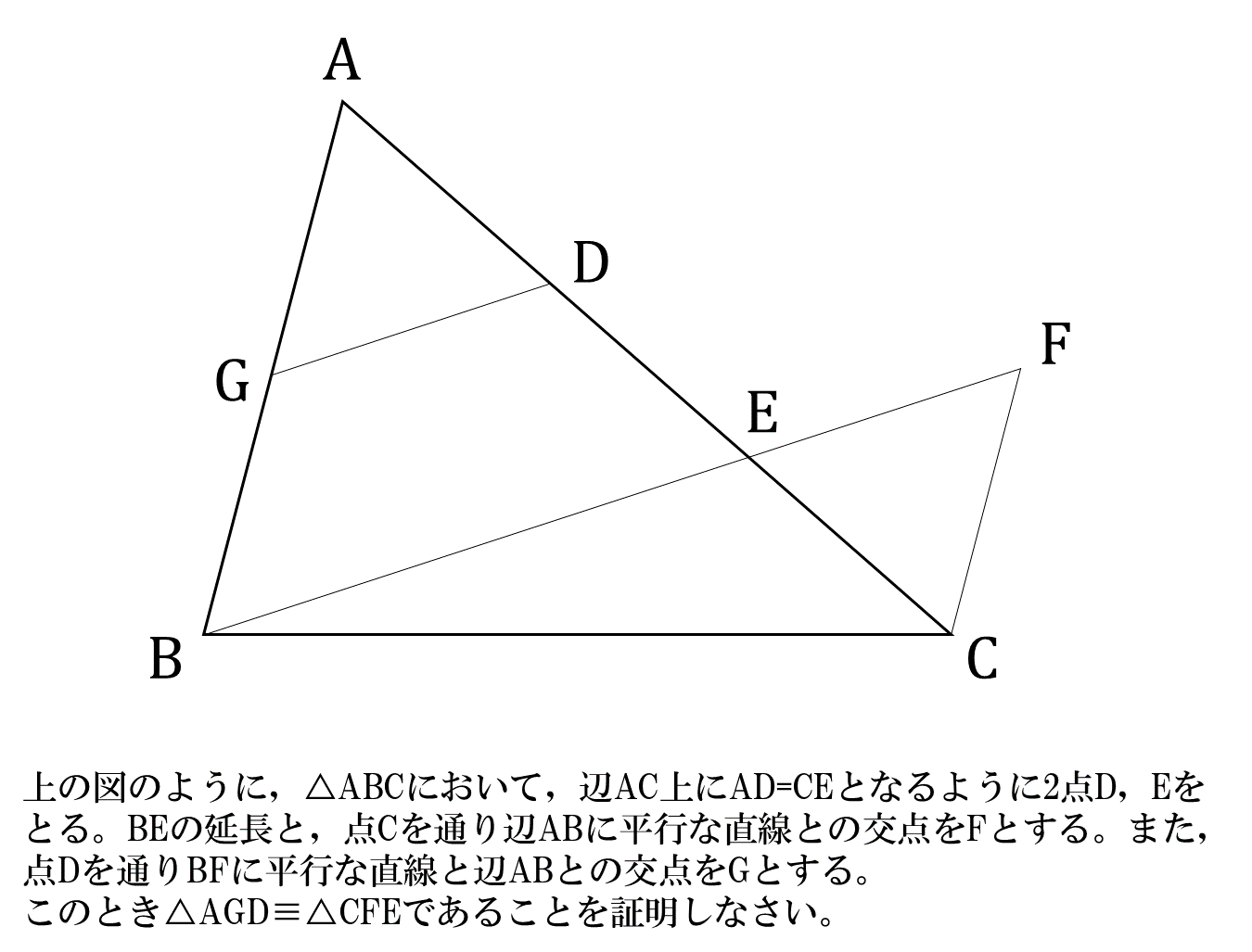


数学 中学証明問題を解く4つのポイント
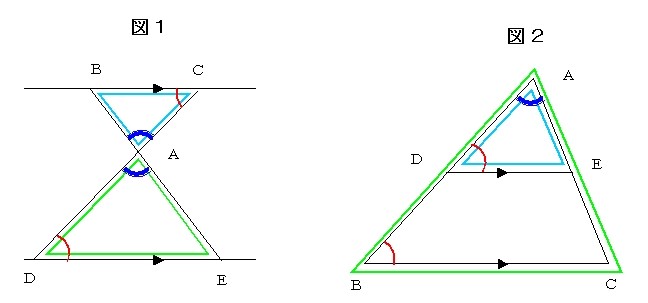


相似 直角三角形
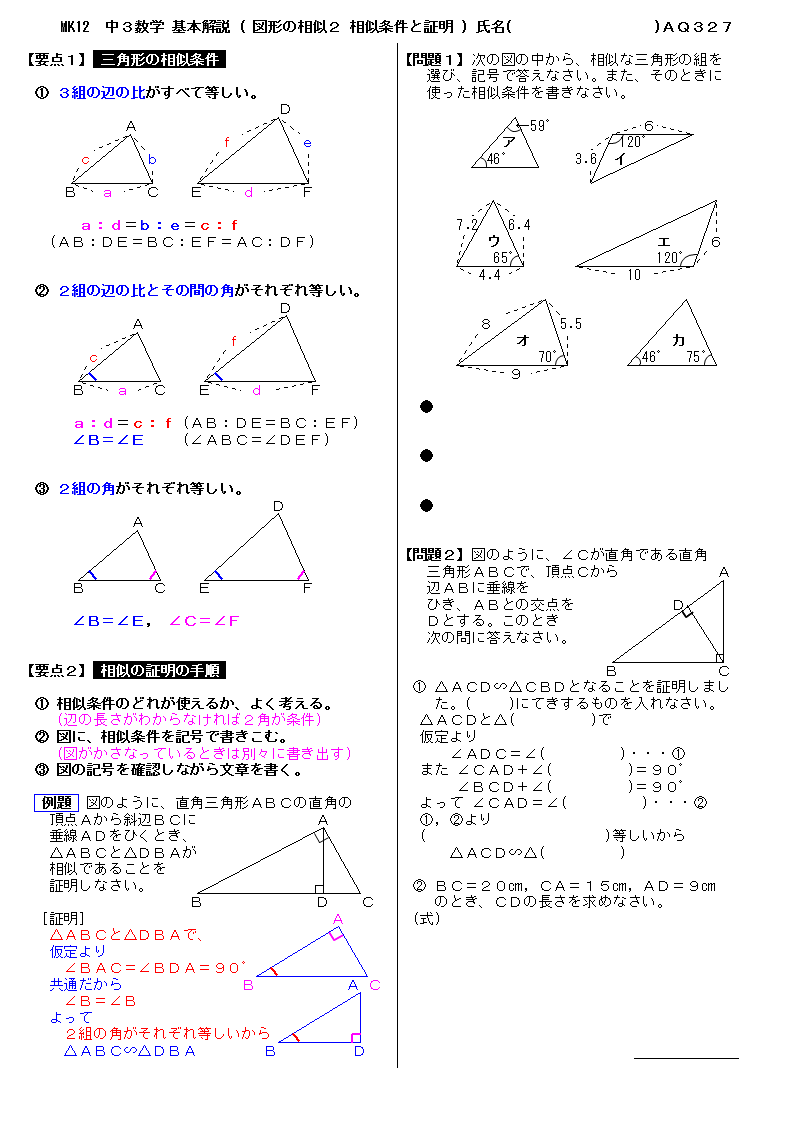


無料 中3数学 基本解説 問題プリント 327 図形の相似2 相似条件と証明



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



相似の証明です 右のこの問題でなぜ Dbfで f 中学数学に関する質問 勉強質問サイト
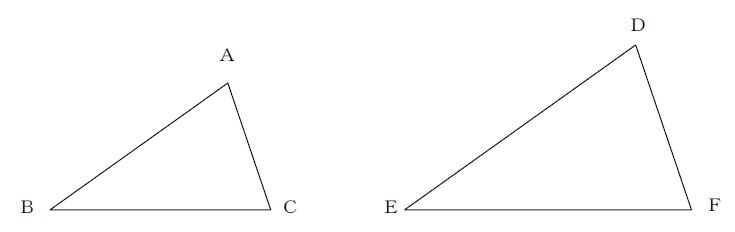


中3数学 相似な図形と相似条件のポイントまとめ やすひこ先生の中学生授業log
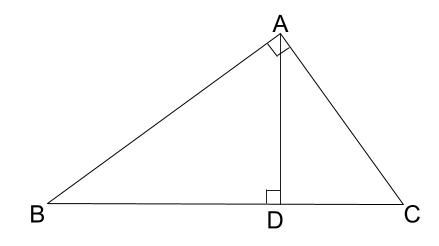


中学数学 相似の証明 その2 中学数学の無料オンライン学習サイトchu Su


直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ



5章1節2 三角形の相似条件2 数学のすすめ


相似の証明問題でマスターしておきたい3つのパターン Qikeru 学びを楽しくわかりやすく



三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張


本時のねらい 図形の中から相似な三角形を見出し 相似条件を用いて証明することができる Ppt Download


相似な図形 証明に慣れよう 苦手な数学を簡単に



中3数学 相似の証明問題 練習編 映像授業のtry It トライイット



中3数学 相似な図形 三角形の相似条件を使った証明 2組の辺の比とその間の角がそれぞれ等しい 三角形の中にある三角形との相似の証明 Youtube
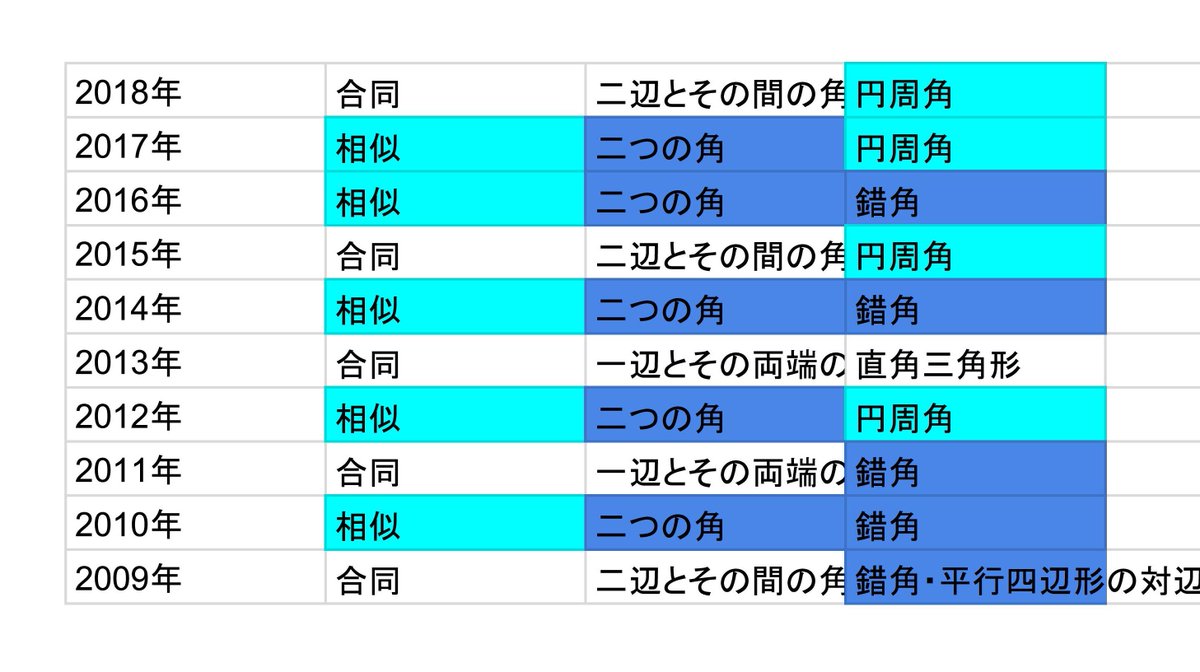


まなびの森 富士見ヶ丘 都立高校入試 数学 大問4 の 証明問題 ではこのように 三角形の合同 と 相似 しか出題されないのだが 注目すべきはこの10年の過去問を分析すると相似が出題された5回のうち 相似条件 は 2つの角が等しい しか使われてい


